Mini
[틀림] 백준 20181 꿈틀꿈틀 호석 애벌레 // 투포인터 dp 본문
https://www.acmicpc.net/problem/20181
* 시도1
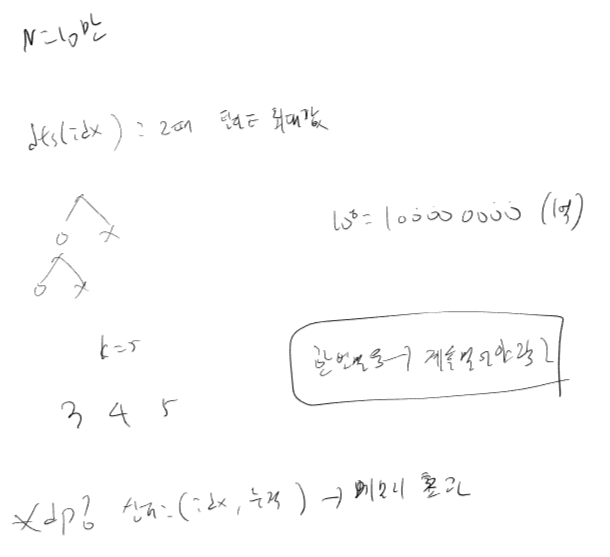
완전탐색방법
상태 : index, 축적된에너지, 얻은탈피에너지, 이전에얻었는지(한번먹으면 계속먹어야함)
O X로 완전탐색
import java.io.*;
import java.util.*;
public class Main {
static long ret, n, k;
static long[] dp = new long[100000+4];
static ArrayList<Long> arr = new ArrayList<>();
// 축척된에너지, 얻은탈피에너지
static void dfs(int idx, long acc, long tal, boolean flag) {
if(acc >=k){
tal += acc-k;
acc=0;
flag=false;
}
if(idx==n){
ret=Math.max(ret,tal);
return;
}
dfs(idx+1,acc + arr.get(idx), tal,true); //선택
if(!flag)
dfs(idx+1,acc, tal,false); //미선택
}
public static void main(String[] args) throws IOException {
Scanner sc = new Scanner(System.in);
Arrays.fill(dp,-1);
n = sc.nextInt();
k = sc.nextInt();
for(int i=0;i<n;++i){
int tmp = sc.nextInt();
arr.add((long) tmp);
}
dfs(0,0,0,false);
dfs(0,0,0,true);
System.out.println(ret);
}
}효용성 : N=10만에서 시간초과
시도2
dp? 상태에 축적값을 저장한다면, 메모리 초과
정답1
이문제는 관찰을 통한 발상이 필요함.
st가 정해진경우, end도 결정된다는 특징을 이용해야함.
파란막대를 그렸을때, 합이 k이상되는 지점에서 멈추고 차이값을 energy에 더하기


dfs를 돌때, 내부에서 반복문을 통해 index부터 탐색해서 저 파란막대를 찾으면, 상태를 저장할 필요없음
찾았으면, 다음 index를 end+1로 하고 다시 dfs 탐색.
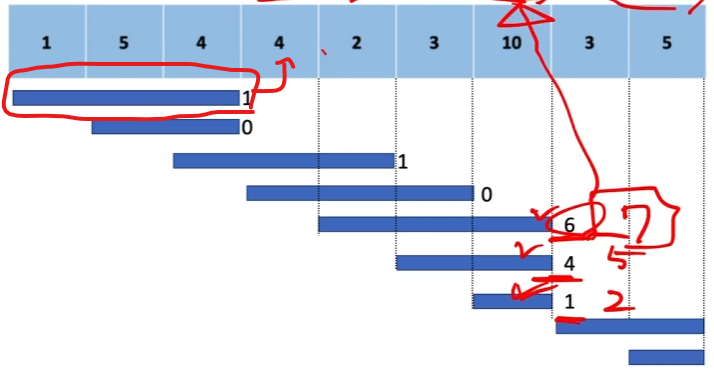
끝에서는 0을 리턴하고, 대신 totalEnergy변수에 파란막대의 값을 저장해놓는다.
import java.io.*;
import java.util.*;
public class Main {
static int n;
static long k;
static long[] satisfaction;
static long[] dp;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
k = Long.parseLong(st.nextToken());
satisfaction = new long[n];
st = new StringTokenizer(br.readLine());
for (int i = 0; i < n; i++) {
satisfaction[i] = Long.parseLong(st.nextToken());
}
// dp[i]: i번째 인덱스부터 시작했을 때 최대 탈피 에너지
dp = new long[n + 1];
Arrays.fill(dp, -1);
System.out.println(dfs(0));
}
// idx 위치부터 시작해서 얻을 수 있는 최대 탈피 에너지
static long dfs(int idx) {
// 기저 조건: 모든 먹이를 고려한 경우
if (idx >= n) {
return 0;
}
// 이미 계산된 결과가 있으면 재사용
if (dp[idx] != -1) {
return dp[idx];
}
// 1. 현재 위치에서 먹기 시작하는 경우
long maxEnergy = 0;
// tryEatingFrom 함수의 내용을 여기로 이동
long totalEnergy = 0;
long accSatisfaction = 0;
int endIdx = idx;
// 연속적으로 먹으면서 만족도 누적
while (endIdx < n) {
accSatisfaction += satisfaction[endIdx];
// 최소 만족도를 달성한 경우
if (accSatisfaction >= k) {
// 탈피 에너지 계산
long energy = accSatisfaction - k;
totalEnergy += energy;
// 다음 위치부터 최대 탈피 에너지 계산해서 더함
totalEnergy += dfs(endIdx + 1);
break;
}
endIdx++;
}
maxEnergy = totalEnergy;
// 2. 현재 위치의 먹이를 건너뛰는 경우
maxEnergy = Math.max(maxEnergy, dfs(idx + 1));
// 결과 저장 및 반환
return dp[idx] = maxEnergy;
}
}
* 정답2
표dp
실전에서 위와같은 dfs로 풀기는 사실 어려울것
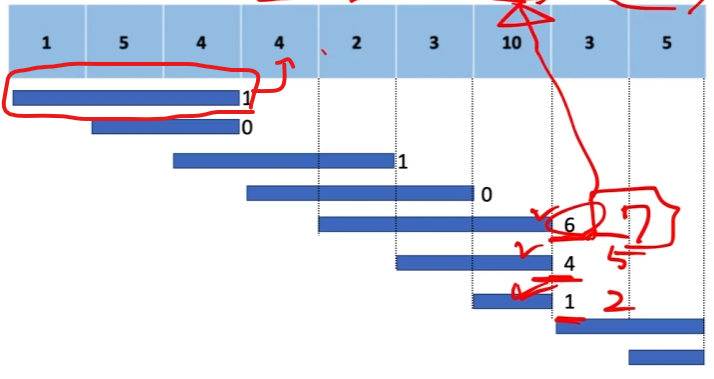
풀이는 다음과 같다.
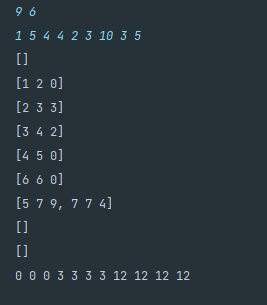
1. 각각의 배열에대해 미리 interval[R] : L,R, 만족감을 저장해놓기 // 그림을 배열에 저장해놓기
이때, dp는 1-idx가 훨씬편하다. l=1, r=0부터 시작해서, r을 하나씩 늘려가면서 합을구하기
결과 : interval[3] : (3,1) (끝나는지점, 값) ( 3,0) ...
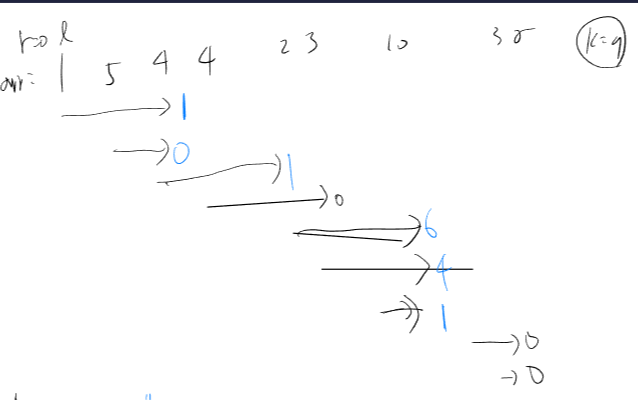
2. dp[i] = i번까지 먹었을때 최대 만족도 =
max ( i-1번까지 얻은 최대만족도 그대로 가져가고, i번은 안먹기 vs i번까지 추가로 먹어서 만족도 얻기)
= max ( dp[i-1] + 0, 이전막대중 최대값 + 현재 먹이값 )

import java.io.*;
import java.util.*;
public class Main {
static class Item {
int left;
long satisfy;
}
static int n, k;
static int[] arr;
static long[] dp;
static List<Item>[] list;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
k = Integer.parseInt(st.nextToken());
arr = new int[n + 1];
st = new StringTokenizer(br.readLine());
for (int i = 1; i <= n; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
// dp[i] : i번째 먹이까지 먹어서 얻을 수 있는 최대 탈피 에너지
dp = new long[n + 1];
list = new ArrayList[n + 1];
for (int i = 1; i <= n; i++) {
list[i] = new ArrayList<>();
}
long sum = 0;
for (int l = 1, r = 0; l <= n; l++) {
// r을 하나씩 늘려보면서 먹을 수 있다면 sum에 축적한다.
while (r + 1 <= n && sum < k) {
sum += arr[++r];
}
// r 에서 끝나는 위치의 정보들을 List에 담아준다.
if (sum >= k) {
Item item = new Item();
item.left = l;
item.satisfy = sum - k;
list[r].add(item);
}
sum -= arr[l];
}
for (int r = 1; r <= n; r++) {
// r번지 음식을 안먹는다면
dp[r] = dp[r - 1];
// r번지 음식을 먹는다면
for (Item item : list[r]) {
// 그전 까지 잘 먹고, 이번에 이 막대를 먹어서 생기는 에너지와의 최댓값
dp[r] = Math.max(dp[r], dp[item.left - 1] + item.satisfy);
}
}
System.out.println(dp[n]);
}
}
헤멨던부분
투포인터 오류
오답코드. 심지어 O(N^2)임.
Long sum=0L;
while(en<=n){
sum += arr[en];
// System.out.println(sum);
if(sum<k){
en++;
}
else{
A a = new A(st, en, sum-k);
intervals[en].add(a);
sum-=arr[st];
sum-=arr[en];
st++;
en=st;
}
}

정답코드. simple is best
Long sum=0L;
for (int l = 1, r = 0; l <= n; l++) {
// r을 하나씩 늘려보면서 먹을 수 있다면 sum에 축적한다.
while (r + 1 <= n && sum < k) {
sum += arr[++r];
}
// r 에서 끝나는 위치의 정보들을 List에 담아준다.
if (sum >= k) {
A item = new A(l,r,sum-k);
intervals[r].add(item);
}
sum -= arr[l];
}시간복잡도는 O(2 * N)임. r이 다시 l로 돌아올필요없음. 쭉 증가만 시키면됨. r은 무조건 증가만 함!!



정리
dp테이블을 정의
시작점에따라 얻는에너지는 결정된다는 점을 관찰. 시각화.
파란화살표 구할때도 투포인터로 O(N)만에 구해야함 (r은 증가만한다는 사실 이용)
점화식 세워서 처리
'Algorithm > dp' 카테고리의 다른 글
| 백준 10653 마라톤2 // dp, 조합대신 점프 idea (0) | 2025.06.05 |
|---|---|
| [세모] 프로그래머스 완전범죄 // dp, void dfs dp (0) | 2025.05.13 |
| [틀림] 백준 문자열 지옥에 빠진 호석 // 문자열, 먼저계산 dp, dfs (0) | 2025.05.12 |
| [맞음] 백준 2156 포도주시식 // dp (0) | 2025.04.29 |
| [틀림] 백준 1480 보석모으기 // 가방여러개 dp (0) | 2025.04.24 |




