Mini
[알고리즘] 백준 1202 보석도둑 // 그리디, pq 본문
https://www.acmicpc.net/problem/1202
* 추론과정
문제는 보석 도둑 문제인데, 각 보석은 무게와 가격을 가지고 있고, 가방에는 각각 최대 무게가 있어서 각 가방에 최대 한 개의 보석을 넣을 수 있다. 우리의 목표는 훔칠 수 있는 보석들의 최대 가격 합을 구하는 거다.
일단, 가장 먼저 생각나는 접근은 그리디 알고리즘일 것 같다. 왜냐하면 최적의 선택을 단계적으로 해나가야 하기 때문이다. 그리디로 풀기 위해서는 어떤 기준으로 선택을 해야 할지 결정해야 한다.
보석을 가격이 높은 순서대로 정렬하고, 각 보석을 담을 수 있는 가장 작은 가방에 넣는 방법이 있지 않을까? 예를 들어, 가장 비싼 보석부터 차례대로 해당 보석의 무게를 수용할 수 있는 가장 작은 가방에 배정하는 거다. 이렇게 하면 가방을 효율적으로 사용할 수 있을 것 같다. 왜냐하면 큰 가방을 나중에 더 큰 보석을 위해 남겨둘 수 있기 때문이다.
그러면 이 과정을 어떻게 구현할 수 있을까?
1. 보석들을 가격이 높은 순서대로 정렬한다. 가격이 같은 경우 무게가 가벼운 순으로 정렬할 필요가 있을까? 아니면 가격 순으로만 하면 될까? 아마 가격이 높은 순으로 정렬하면 될 것 같다. 왜냐하면 가격이 높은 걸 먼저 처리하는 게 이득이니까.
2. 가방들을 오름차순으로 정렬한다. 그리고 각 보석을 처리할 때 해당 보석의 무게보다 크거나 같은 가방 중에서 가장 작은 가방을 선택해야 한다. 이때, 이미 사용한 가방은 제외해야 한다.
여기서 중요한 건, 보석의 무게를 담을 수 있는 가방 중 가장 작은 것을 선택하는 것인데, 이는 이진 탐색을 통해 가능할 것 같다. 가방들을 정렬해놓고, lower_bound 같은 함수로 해당 보석의 무게보다 크거나 같은 가장 작은 가방을 찾는 거다. 그리고 그 가방을 사용 처리하면 된다.
하지만 가방을 효율적으로 관리하기 위해서는 어떤 자료구조를 사용해야 할까? 가방을 정렬된 상태로 유지하고, 사용 가능한 가방 중에서 조건을 만족하는 가장 작은 것을 찾아야 한다. 예를 들어, 가방들을 정렬한 뒤, 각 보석에 대해 이진 탐색으로 가능한 가방을 찾고, 그 가방을 제거하는 방식이면 될 것 같다.
그러나 N과 K가 최대 30만까지 가능하기 때문에, 이진 탐색으로 찾고 가방을 제거하는 과정이 O(K) 시간이 걸리면 안 된다. 그래서 더 효율적인 방법이 필요하다.
이를 위해서는 TreeSet 같은 자료구조를 사용할 수 있는데, Python에서는 기본적으로 제공되지 않는다. 하지만 이진 검색을 이용해서 가능한 방법을 찾아야 한다.
예를 들어, 가방을 정렬한 후, 각 보석에 대해 이진 검색으로 해당 무게 이상의 가장 작은 가방을 찾고, 그 가방을 제거하는 방식으로 진행한다. 그런데 이진 검색 후에 요소를 제거하는 것이 O(1) 시간에 가능하려면 리스트가 아니라 다른 구조를 사용해야 하는데, Python의 경우 list에서 이진 검색은 bisect 모듈을 사용할 수 있지만, 요소를 제거할 때 O(1) 시간이 아닌 O(n) 시간이 걸린다. 따라서 이 방법은 K가 3e5일 경우 O(K^2) 시간이 걸려서 시간 초과가 날 것이다.

그럼 다른 방법이 필요하다. 이 문제를 해결하기 위해 우선순위 큐나 힙을 사용할 수 있는 방법이 있을까?
다른 접근법을 생각해보자.
보석을 무게가 작은 순으로 정렬하고, 가방도 작은 순으로 정렬한다. 그리고 각 가방에 대해 담을 수 있는 보석 중 가장 가치가 높은 것을 선택하는 방식이다.
예를 들어, 가방을 작은 것부터 처리한다. 각 가방에 담을 수 있는 모든 보석들을 모아서 그 중 가장 가치가 높은 것을 선택하는 것이다. 이렇게 하면 가방이 작은 것부터 처리되기 때문에 남은 보석 중에서 최대 가치를 선택할 수 있다.
이 방법은 다음과 같이 구현할 수 있다:
1. 보석을 무게 기준으로 오름차순 정렬한다.
2. 가방을 오름차순으로 정렬한다.
3. 각 가방을 순회하면서, 해당 가방의 최대 무게보다 작거나 같은 모든 보석들을 우선순위 큐(최대 힙)에 넣는다.
4. 우선순위 큐에서 가장 가치가 높은 보석을 선택하여 결과에 더한다.
이 방식은 각 가방을 처리할 때마다 해당 가방에 넣을 수 있는 보석들을 모아 최대 가치를 선택하는 방식이다.
이 방법의 시간 복잡도는 보석 정렬 O(N log N), 가방 정렬 O(K log K), 그리고 각 가방을 처리할 때 보석을 우선순위 큐에 넣는 과정이 O(N log N)이 될 수 있다. 하지만 가방과 보석을 한 번씩만 처리하므로 O(N + K) 정도의 시간이 걸릴 수 있다.
이 방법이 더 효율적일 것 같다. 왜냐하면 보석과 가방을 정렬한 후 각 가방에 대해 가능한 보석들을 최대 힙에 추가하고, 각 단계에서 최대 가치를 선택하는 방식이기 때문이다.
예를 들어, 예제 입력 2를 보면:
보석 목록:
1 65
5 23
2 99
가방은 10, 2.
보석을 무게 순으로 정렬하면 (1,65), (2,99), (5,23). 가방은 [2,10]으로 정렬된다.
처음 가방 2를 처리할 때, 무게가 2 이하인 보석은 (1,65), (2,99)가 된다. 이들을 가격 기준 최대 힙에 넣으면 99가 선택되어 결과에 99 추가.
두 번째 가방 10을 처리할 때, 남은 보석 중 무게가 10 이하인 것은 (5,23)이 있지만 이미 처리된 보석인지 확인해야 한다. 하지만 이 방식에서는 보석을 한 번만 처리하기 때문에, 앞의 두 보석은 이미 처리되었을까?
아니다. 이 방식에서는 각 가방을 처리할 때, 현재까지의 보석 포인터를 유지한다. 예를 들어, 보석 포인터 i를 0부터 시작해서, 각 가방의 무게 Ci에 대해, Mi <= Ci인 모든 보석을 우선순위 큐에 넣는다. 즉, i를 Ci가 증가하는 순서로 가방을 처리하면서, 보석을 i까지 증가시키며 우선순위 큐에 추가한다.
예를 들어, 가방이 [2,10]으로 정렬되면, 첫 번째 가방은 2이다. 보석을 무게 순으로 정렬했으므로, Mi <= 2인 보석은 (1,65)와 (2,99)이다. 이들을 우선순위 큐에 넣고, 가장 큰 가치인 99를 선택.
그 다음 가방은 10이다. Mi <=10인 보석은 5까지 가능. 현재 i는 2까지 처리되었으므로, 5인 보석도 큐에 추가. 그러면 우선순위 큐에는 65,99,23 중 99는 이미 선택되어 없고, 65와 23이 남아있을까?
아니다. 여기서 문제는 보석을 한 번만 처리해야 한다. 즉, 보석은 한 번만 우선순위 큐에 들어가야 한다.
이 방식의 정확한 과정은:
- 보석을 무게 오름차순으로 정렬.
- 가방을 오름차순으로 정렬.
- 보석을 가리키는 포인터 j를 0에서 시작.
- 각 가방 c_i에 대해, j를 증가시키며 보석[j]의 무게가 c_i 이하인 모든 보석을 우선순위 큐(최대 힙)에 추가.
- 우선순위 큐에서 가장 큰 값을 꺼내어 결과에 더함.
이렇게 하면 각 보석은 정렬되어 있으므로, j는 계속 증가하며 중복 처리되지 않는다.
예제 2의 경우:
보석: (1,65), (2,99), (5,23) → 무게 순 정렬.
가방: [2,10] → 오름차순 정렬.
처리 순서:
가방 2 처리:
j=0 → 보석 무게 1 <=2 → 힙에 65 추가. j=1 → 보석 무게 2 <=2 → 힙에 99 추가. j=2 → 보석 무게 5>2 → 중지.
힙에서 최대값 99를 꺼내서 합에 추가. → 합 99.
가방 10 처리:
현재 j=2. 보석 무게 5 <=10 → 힙에 23 추가. j=3인데 보석이 3개이므로 중지.
힙에서 최대값 65를 꺼내서 합에 추가. → 합 99+65=164.
하지만 보석 65는 아직 처리가 안 된 것 아닌가?
아, 그렇다. 첫 번째 가방 처리에서 99를 꺼내고, 두 번째 가방 처리에서는 우선순위 큐에 65와 23이 남아 있으므로 최대값 65를 선택한다.
따라서 예제 2의 결과는 99+65=164가 맞다.
이 방법이라면 시간 복잡도는 O(N log N + K log K + (N + K) log N) 정도가 될 것 같다.
보석 정렬 O(N log N), 가방 정렬 O(K log K). 그리고 각 가방 처리 시 보석을 j까지 추가하는데, 전체 보석은 한 번만 스캔하므로 O(N)이다. 각 보석을 힙에 넣는 것은 O(log N) 시간이 걸리고, K번의 힙 추출이 O(log N) 시간이므로 전체적으로 O(N log N + K log K + (N + K) log N)이 된다.

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n,k,ret;
vector<pair<int,int>> v; // < 무게, 가격 >
vector<int> bag; // 가방무게들
priority_queue<int,vector<int>> pq; // 최대힙
int main(){
ios_base::sync_with_stdio(0);
cin.tie(0);
cin>>n>>k;
for (int i=0;i<n;++i) {
int a,b;
cin>>a>>b;
v.push_back({a,b});
}
for (int i=0;i<k;++i) {
int a;
cin>>a;
bag.push_back(a);
}
// 보석 무게순 정렬
sort(v.begin(),v.end());
//가방 오름차순정렬
sort(bag.begin(), bag.end());
//각 가방에 대해
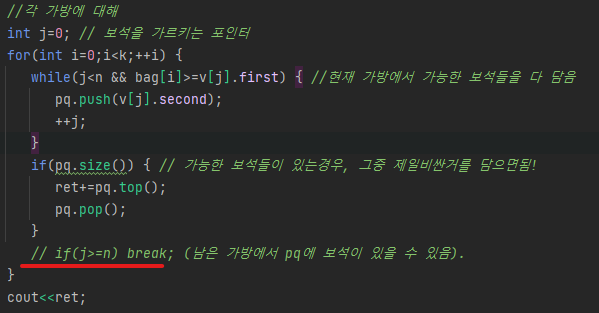
int j=0; // 보석을 가르키는 포인터
for(int i=0;i<k;++i) {
while(j<n && bag[i]>=v[j].first) { //현재 가방에서 가능한 보석들을 다 담음
pq.push(v[j].second);
++j;
}
if(pq.size()) { // 가능한 보석들이 있는경우, 그중 제일비싼거를 담으면됨!
ret+=pq.top();
pq.pop();
}
// if(j>=n) break; (남은 가방에서 pq에 보석이 있을 수 있음).
}
cout<<ret;
return 0;
}
* 시행착오들
- q 접근전에 size 체크안한것

- 이상한 탈출조건
- 큰수는 long long 박고 시작할것.

'Algorithm > greedy' 카테고리의 다른 글
| [알고리즘] 프로그래머스 요격시스템 // 그리디 (0) | 2025.02.06 |
|---|---|
| [알고리즘, 틀림] 백준 1700 멀티탭 스케쥴링 // 그리디, 페이지 교체 알고리즘 (0) | 2025.02.01 |
| [알고리즘] 백준 1931 회의실 배정 // 그리디, 라인스위핑, 정렬 (0) | 2025.01.28 |
| [알고리즘] 백준 14469 // 그리디, 라인스위핑은 막대기를 그려라 (0) | 2025.01.28 |
| [알고리즘] 백준 1787 컵라면 // 그리디 , pq (0) | 2025.01.27 |




