Mini
[알고리즘] 백준 15926 현욱은 괄호왕이야 // stack, 괄호검사 심화 본문
https://www.acmicpc.net/problem/15926
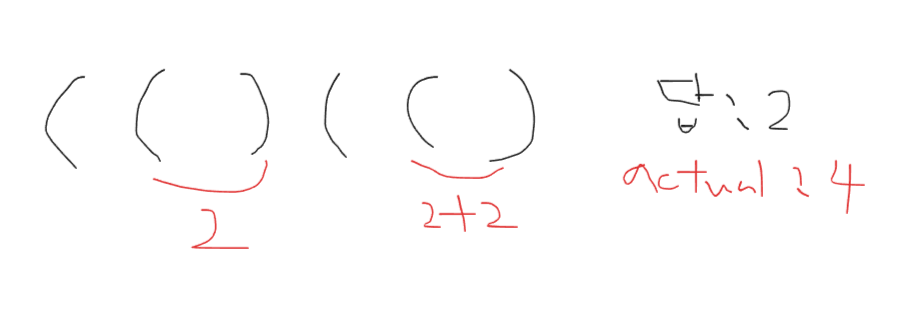
* 풀이1
- 우측괄호를 만나면 cnt+=2 하는 풀이
- 문제점
- 중간에 ( 가 낑겨있는 경우 를 고려못함.
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int n,ret;
stack<char> stk;
string s;
int main(){
ios_base::sync_with_stdio(0);
cin.tie(0);
cin>>n>>s;
int cnt=0;
for(auto c : s) {
// cout<<cnt<<" ";
if(c=='(') {
stk.push(c);
}
else if(c==')' && stk.empty()){
cnt=0;
}
else if(c==')' && stk.size() && stk.top()=='('){
cnt+=2;
stk.pop();
ret=max(ret,cnt);
}
}
cout<<ret;
return 0;
}
* 풀이2
- 상태를 배열에 저장함
- stack에 index를 push
- 우측괄호를 만난경우, 현재와 top의 index의 배열값을 1로 저장
- d[i] = d[stk.top()] = 1로 구현

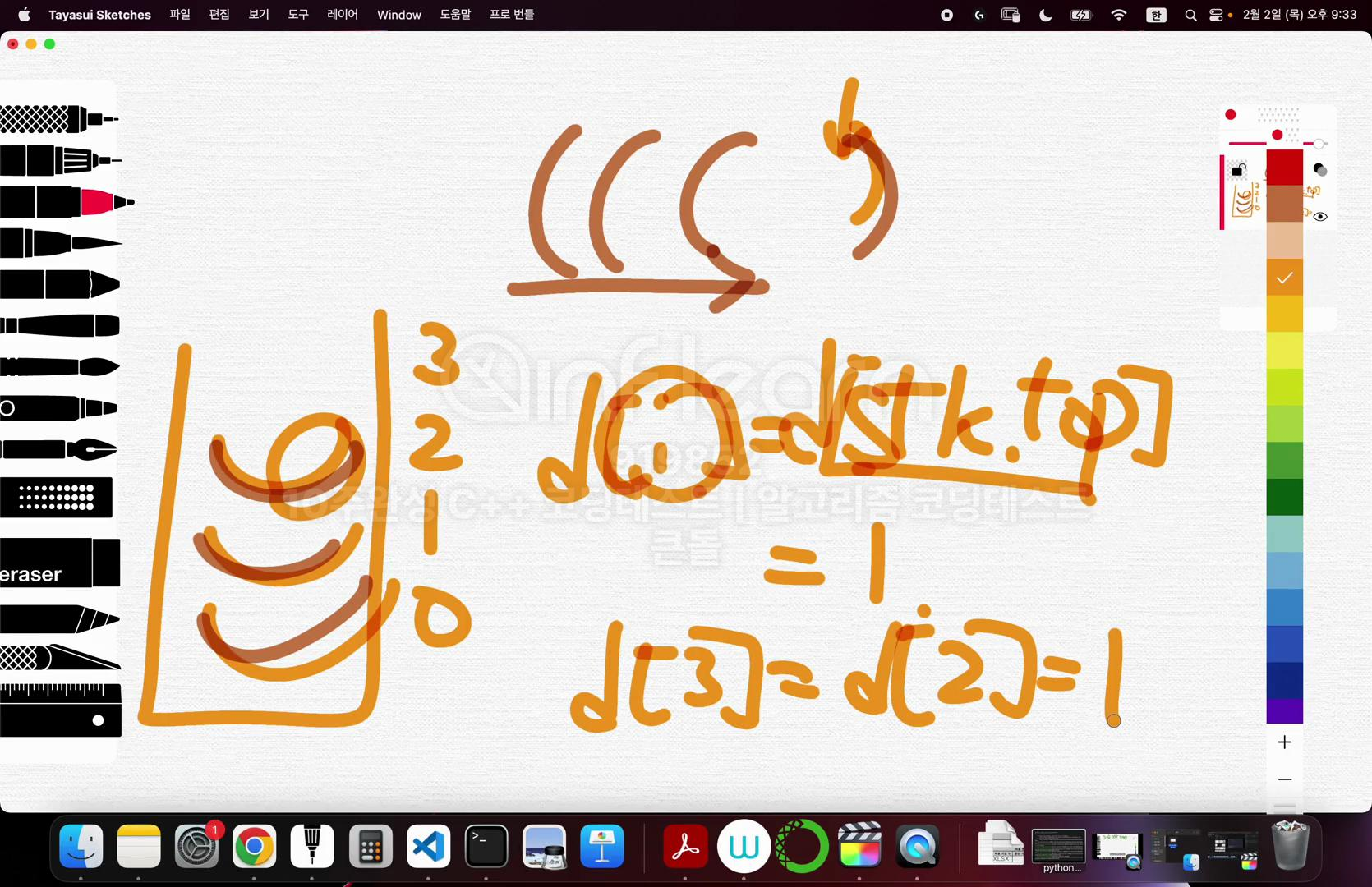
- 마지막 배열을 순회하면서 연속된 1의 최대값을 찾으면 된다.
- 주의
- 1을 만날때마다 정답갱신해야함
- 0을 만날때 갱신하면 누락

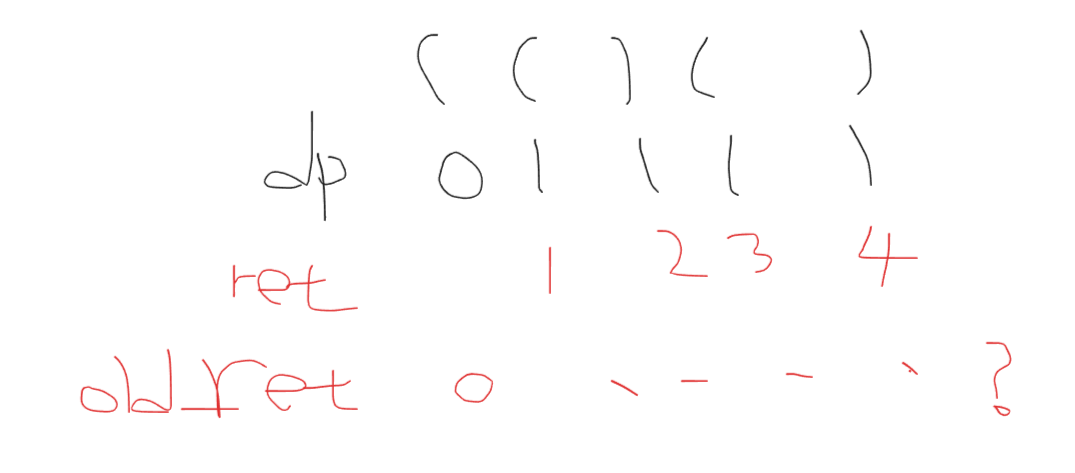
* 전체코드
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int n,ret, dp[200000+4];
stack<int> stk;
string s;
int main(){
ios_base::sync_with_stdio(0);
cin.tie(0);
cin>>n>>s;
for(int i=0;i<n;++i) {
// cout<<cnt<<" ";
if(s[i]=='(') {
stk.push(i);
}
else if(s[i]==')' && stk.size()){
dp[i]=1;
dp[stk.top()]=1;
stk.pop();
}
}
int cnt=0;
for(int i=0;i<n;++i) {
if(dp[i]) {
cnt++;
ret=max(ret,cnt);
}
else {
cnt=0;
}
}
cout<<ret;
return 0;
}
* 결론
- stack에 index를 push 하라
- ) 을 만날때마다 배열에 기록 (현재, top)
* 풀이3
- dp 배열도 안쓰는 풀이
- 우측괄호를 만난경우, pop을하고, i - top 을 하면 최장 괄호 길이가 나옴
- ex) 3일때, 2pop, 3-1 = 2
- 4일때, 1pop, 4-0 = 4
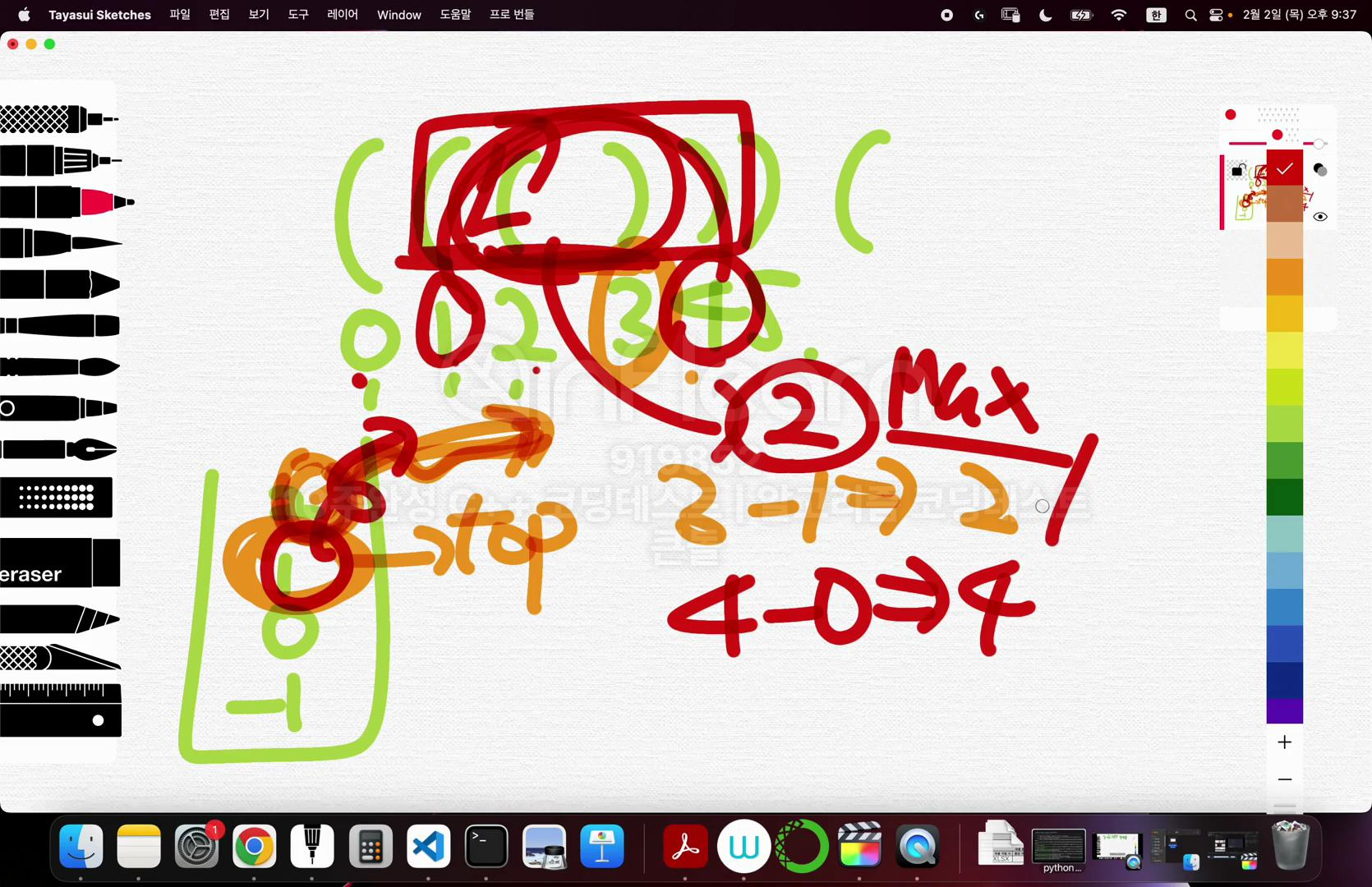
- stack에 -1을 넣는이유
- 5가 들어왔을때 , pop0, 5-(-1) = 6 하기 위해
- 빈경우, push를 하는이유
- 새로운 분기점을 만들기 위해
- ex) 5를 push 해야 뒤에 새로운 7 이 왔을때, 6pop, 7-5 = 2로 계산을 할수있음.
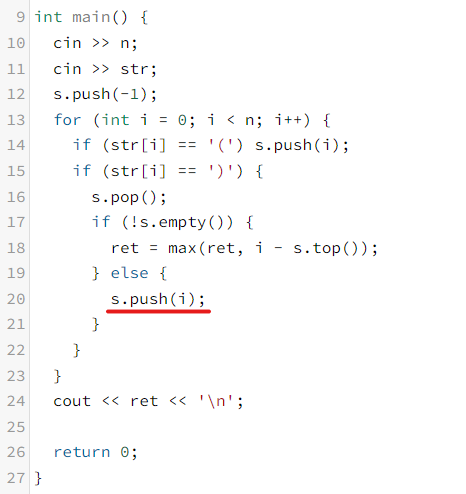

#include <bits/stdc++.h>
using namespace std;
int n, cnt, ret;
string str;
stack<int> s;
int main() {
cin >> n;
cin >> str;
s.push(-1);
for (int i = 0; i < n; i++) {
if (str[i] == '(') s.push(i);
if (str[i] == ')') {
s.pop();
if (!s.empty()) {
ret = max(ret, i - s.top());
} else {
s.push(i);
}
}
}
cout << ret << '\n';
return 0;
}'Algorithm > 스택' 카테고리의 다른 글
| [알고리즘] 백준 6549 히스토그램 // 스택 심화, 암기.. (0) | 2025.01.19 |
|---|---|
| [알고리즘] 백준 3015 오아시스 재결합 // 스택 심화 (0) | 2025.01.19 |
| [알고리즘] 백준 1725 히스토그램 // 스택 (0) | 2024.12.29 |
| [알고리즘] 백준 6198 옥상정원꾸미기 // 스택, 역발상, 자기중심적 사고, st.size() 도 의미가 있다. (0) | 2024.12.29 |
| [알고리즘] 백준 17299 오등큰수 // 스택 (0) | 2024.12.28 |




