Mini
리트코드 211 c++ // 트라이 와일드카드 종결, 재귀vs길이별 트라이 본문
1. 와일드카드가 처음, 중간, 끝에 있는경우 모두 커버하는 코드
1. 삽입부분은 기존과 동일하다.
2. 검색에서 재귀함수를 써야한다.
bool search(const string& word, int index) const { //끝에const => 이함수에서는 클래스내부 변수 수정금지
if (index == word.size()) { //문자끝에 온경우
return isEnd;
}
char c = word[index];
if (c == '.') {
for (int i = 0; i < 26; ++i) { //.이면 모든알파벳을 검사해야함, 하나라도있으면 true임
if (child[i] && child[i]->search(word, index + 1)) {
return true;
}
}
return false; //자식이 하나도없으면 false
}
else { //일반 단어인경우
return child[c - 'a'] && child[c - 'a']->search(word, index + 1);
}
}입력이 "b.."일때 재귀함수의 구조를 보고 코드를 이해해보자.
search("b..", 0)
|
Trie at root (cur)
c = 'b' |
|
child['b'-'a'] != nullptr
|
search("b..", 1) at node 'b'
|
Trie at 'b' (cur->child['b'-'a'])
c = '.' (wildcard)
Iterate over children[0..25]
|
search("b..", 2) at node 'a'
|
Trie at 'a' (cur->child['a'-'a'])
c = '.' (wildcard)
Iterate over children[0..25]
|
search("b..", 3) at node 'd'
|
Trie at 'd' (cur->child['d'-'a'])
index == word.size()
return isEnd (true)3. 전체코드
class WordDictionary {
class Trie {
public:
bool isEnd;
Trie* child[26];
Trie() : isEnd(false) {
memset(child, 0, sizeof(child));
}
void addWord(const string& word) {
Trie* cur = this;
for (char c : word) {
if (cur->child[c - 'a'] == nullptr) {
cur->child[c - 'a'] = new Trie();
}
cur = cur->child[c - 'a'];
}
cur->isEnd = true;
}
bool search(const string& word, int index) const {
if (index == word.size()) {
return isEnd;
}
char c = word[index];
if (c == '.') {
for (int i = 0; i < 26; ++i) {
if (child[i] && child[i]->search(word, index + 1)) {
return true;
}
}
return false;
} else {
return child[c - 'a'] && child[c - 'a']->search(word, index + 1);
}
}
};
private:
Trie root;
public:
WordDictionary() {}
void addWord(const string& word) {
root.addWord(word);
}
bool search(const string& word) const {
return root.search(word, 0);
}
};
/**
* Your WordDictionary object will be instantiated and called as such:
* WordDictionary* obj = new WordDictionary();
* obj->addWord(word);
* bool param_2 = obj->search(word);
*/2. 카카오문제 : 해당하는 단어의 갯수를 리턴하라는 경우
#include <bits/stdc++.h>
using namespace std;
class Trie {
public:
int isEnd;
Trie* child[26];
Trie() : isEnd(false) {
memset(child, 0, sizeof(child));
}
void insert(const string& word) {
Trie* cur = this;
for (char c : word) {
if (cur->child[c - 'a'] == nullptr) {
cur->child[c - 'a'] = new Trie();
}
cur = cur->child[c - 'a'];
}
cur->isEnd++;
}
int search(const string& word, int index) const { //끝에const => 이함수에서는 클래스내부 변수 수정금지
if (index == word.size()) { //문자끝에 온경우
//ret+=isEnd;
return isEnd;
}
char c = word[index];
if (c == '?') {
int ret=0; //리턴값은 기저사례 이후에 둬야함
for (int i = 0; i < 26; ++i) { //.이면 모든알파벳을 검사해야함, 하나라도있으면 true임
if (child[i]) {
ret+=child[i]->search(word, index + 1);
//return 1;
}
}
return ret; //자식이 하나도없으면 0이 리턴될것임
}
else { //일반 단어인경우
if(child[c-'a']){ //해당 단어자식이 있으면 거기로 들어감, 자식리턴값을 그대로 따름
return child[c-'a']->search(word, index + 1);
//return ret;
}
return 0; //해당 자식이없으면 0 리턴
}
}
};int ret를 두고, ret+=하는 방식으로 수정해야한다.
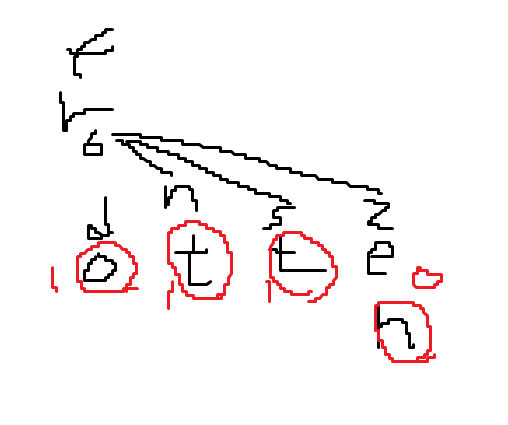
위 그림을 보면, 숫자친부분은 기저사례에 걸려서 리턴되는 숫자이다.
o입장에서 보면, 모든자식들의 리턴값을 더하는 코드를 볼수 있다. (for 0~26)
따라서, o의 리턴값은 1+1+1+0이 되고
밑에서 3번째줄에 의해, 자식이있는경우 자식의 리턴값을 그대로 리턴하도록 되어있다!!
즉, r은 o의 리턴값인 3을 그대로 따른다!
*단점 : 시간복잡도를 굉장히 많이 잡아먹는다.
* 카카오 문제의 경우 중간에 와일드 카드가 없다. -> 즉, 길이별 트라이를 이용해 공간을 쓰고
시간을 줄여야 통과가능하다.
3. 결론(재귀 방식의 단점)
와일드카드가 중간에 있다? -> 재귀 트라이 //최악 : ?????인경우 -> 모든 자식을 봐야함 -> 26 ^ 쿼리갯수 -> 터짐
중간에 와일드카드 없는경우 ->( 재귀트라이로 냈더니 시초) -> 길이별 트라이 구현 // O(쿼리갯수 * 쿼리길이)?
*장점 : 중간에 와카가 나와도 정답
4. 길이별 트라이의 장점
frodo, front, frost를 저장할때, cnt+1하면서 지나가도록 구현하므로,
?를 만난경우 더 깊이 들어가지않고, 그즉시 3을 리턴하므로,
시간복잡도가 굉장히 절약 된다!
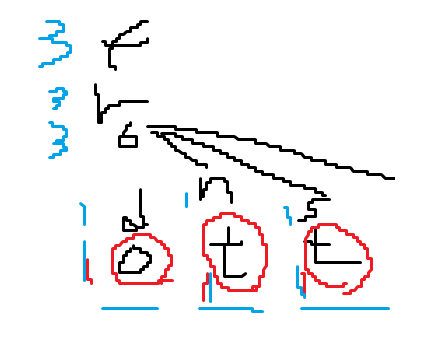
* 단점 : 중간에 와카가 나오면 오답.
'Algorithm > 트라이' 카테고리의 다른 글
| 리트코드 208. Trie 구현 c++ // 트라이복습, c클래스 초기화 방법 (0) | 2024.05.18 |
|---|---|
| 백준 5670 c++ 휴대폰자판 // 트라이 자식수, 소수점출력방법, mx설정방법 (0) | 2024.05.07 |
| 프로그래머스 가사검색 c++ // 정석트라이, 단어 길이별 트라이, 접미사 구하는법, 한계 (0) | 2024.05.03 |
| 프로그래머스 자동완성 c++ // 트라이, 자동완성 결정방법 (0) | 2024.05.02 |
| 백준 5052 전화번호 목록 c++ // 트라이, 서로 접두어검사, 입력값은 모두받아야함 (0) | 2024.05.02 |




