Mini
프로그래머스 도넛과막대그래프 c++ // 그래프 차수 특징발견, 사이클검사방법, 최대번호노드 찾는방법 본문
https://school.programmers.co.kr/learn/courses/30/lessons/258711
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
1. 그래프 차수 특징발견
각 그래프마다 대표정점의 특징(고유한 degree값)이 존재한다.
해당정점의 갯수가 그 그래프의 갯수이다!
0. 모든그래프의 갯수 == 시작점에서 뻗어나가는 간선갯수와 같다.
4에서 위로가는 집합 : a모양
좌로가는 집합 : b모양
우로가는 집합 : c모양이 된다.
즉, 3개의 집합이 도넛인지, 뭔지 찾으면 된다.

1. 도넛그래프
out, indegree가 같다, but 대표정점이 없다. 다른 그래프의 특징관찰후
0번 특성을 이용해 나머지의 갯수로 구해보자.
도넛그래프갯수 = 시작점의
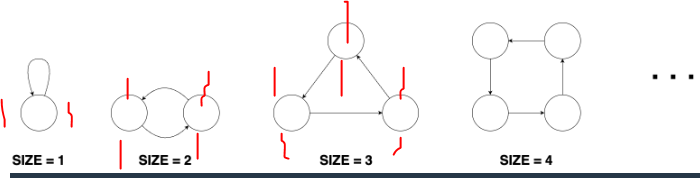
2. 막대그래프
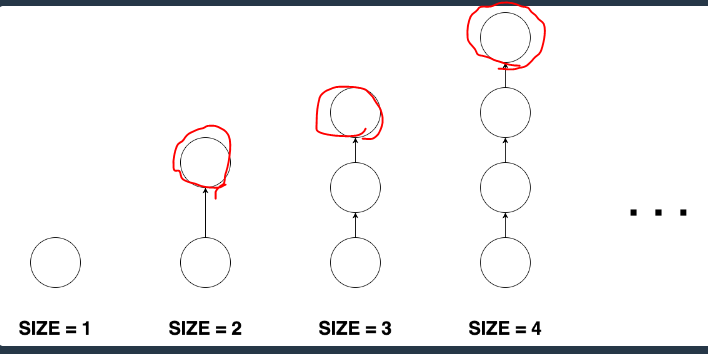
빨간정점의 갯수가 막대그래프의 갯수이다
특징 : in==1 and out==0
3. 8자 그래프
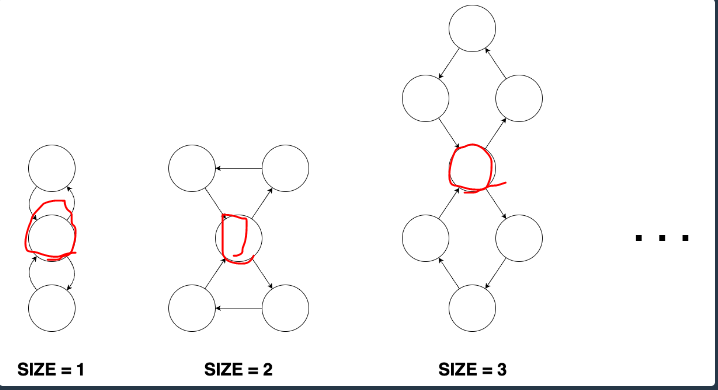
빨간정점의 갯수가 8자 그래프의 갯수이다.
특징 : in>=2 and out >=2
4. 시작점찾기
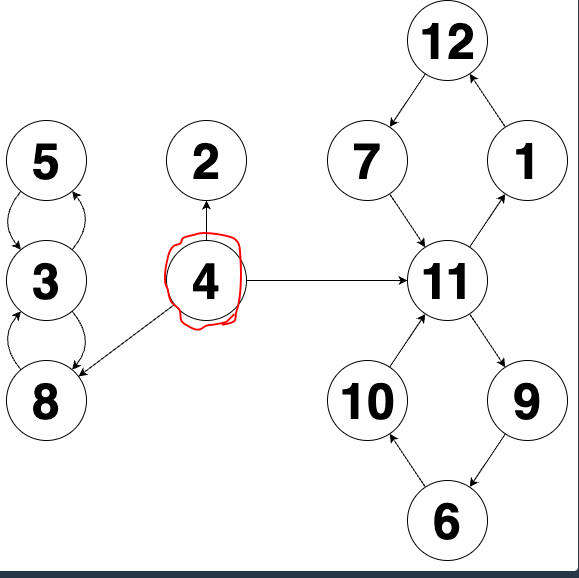
시작점의 특징 : in==0 and out>=2
1.5 최대번호노드 찾는방법
set, pq로 쇼하는거보다 이게낫다.
n = max(n, max(edge[0], edge[1]));
2. 시행착오
카카오 공식해설에는 시작점을 제거하고 막대그래프특징 : out==0 이라고 하는데,
자꾸 35번 tc에서 오답이나서
시작점을 제거안하고, 막대그래프특징 : in==1 and out==0 하니 통과가 됐다...
3. 사이클검사방법
특징을 못찾은경우 사이클 검사해서 푸는방법을 이 기회에 알아보자.
int discovered[101];
bool finished[101];
vector<int> graph[101];
int node_order;
int cycle;
void dfs(int node)
{
// 해당 노드가 몇번째에 방문되었는지 기록
discovered[node] = node_order++;
for (int i: graph[node])
{
if (discovered[i] == -1)
dfs(i);
else if (!finished[i])
++cycle;
// else는 cross edge인 경우
}
// 해당 노드의 함수 호출이 종료되었음을 명시
finished[node] = true;
}위 그래프의 경우 dfs(1), dfs(2), dfs(3)이 차례로 호출된 상태에서 dfs(3)이 1번 노드를 접근하려고 하고 있다.
이때 1번 노드에 방문은 한 상태지만 dfs(1)의 호출은 아직 끝나지 않은 상태이므로 finished[1] == false이며 back edge 판정이 되고 이 그래프는 사이클을 가짐을 알 수 있다.
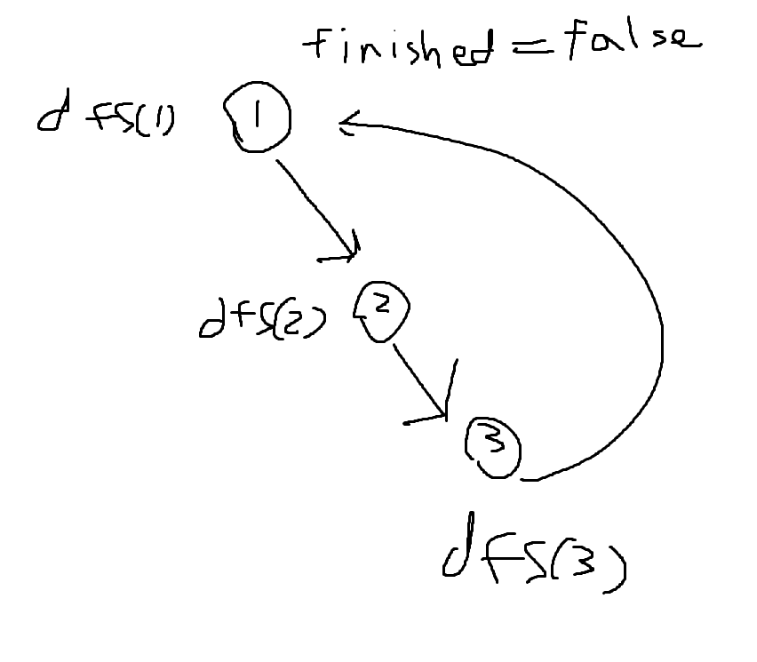
즉, visit됨 and fin=false 이면 사이클이 있는것이다.
4.전체코드
#include <bits/stdc++.h>
using namespace std;
vector<int> adj[1000000+1] ; //노드i의 인접리스트
int indeg[1000000+1],outdeg[1000000+1],vis[1000000+1];
int a,b,c,d,n;
int dfs(int node, int st){
cout<<node<<" ";
//8자?
if(vis[node] && node==st){
return 2;
}
//다음노드봣더니 이미방문됨 -> 사이클
if(vis[node]){
cout<<"도넛\n";
return 1; //도넛
}
for(auto nxt : adj[node]){
if(vis[nxt]) continue;
vis[node]=1;
dfs(nxt,st);
}
return 0;
}
vector<int> solution(vector<vector<int>> edges) {
vector<int> answer;
unordered_set<int> s;
//n=edges.size();
for(auto edge : edges){
adj[edge[0]].push_back(edge[1]);
indeg[edge[1]]++;
outdeg[edge[0]]++;
n = max(n, max(edge[0], edge[1]));
}
for(int i=1;i<=n;++i){
if(outdeg[i]>=2 && indeg[i]==0) a=i;
//막대모양갯수 == indgee가 0인정점갯수
else if(outdeg[i]==0 && indeg[i]>=1) {
//cout<<i<<"\n";
c++;
}
//도넛모양갯수 == in,out이 2이상인 정점의 갯수
//즉! 유일정점의 특징을 발견하고, 그 갯수를 세면된다!
else if(indeg[i]>=2 && outdeg[i]>=2) d++;
}
b=adj[a].size() - (c+d);
//b+c+d == a.adj.size();
//a : indegre 0 and outdegre max
//b : 도넛
//c : 막대
//d : 8자
return answer={a,b,c,d};
}'Algorithm > 그래프' 카테고리의 다른 글
| [틀림] 백준 1167 트리의 지름 // 거리는? bfs, 트리개념 (0) | 2025.03.26 |
|---|---|
| [알고리즘] 리트코드 course schedule // dfs cycle 감지 (0) | 2025.03.06 |
| [알고리즘] 백준 13244 Tree // tree의 조건 암기 (0) | 2025.01.18 |
| 리트코드 133 그래프 클론 c++ // 그래프 복사하는방법 (0) | 2024.05.20 |
| 백준 1717 집합의표현 c++ // 유니온 파인드 구현방법 (0) | 2023.11.29 |



