Mini
[틀림] 백준 1253 좋다 c++ // 이분탐색 발상, 주의점(자기자신예외처리) 본문
https://www.acmicpc.net/problem/1253
1253번: 좋다
첫째 줄에는 수의 개수 N(1 ≤ N ≤ 2,000), 두 번째 줄에는 i번째 수를 나타내는 Ai가 N개 주어진다. (|Ai| ≤ 1,000,000,000, Ai는 정수)
www.acmicpc.net
1. 의사코드
1 2 3 3 3 4
i j LB UB
에서
1. 해당수(a[i]+a[j])가 존재한다면, UB-LB로 그 갯수만큼 더해준다
2. 문제 : 1 2 3 3 3 1 2 인 경우 : 3은 앞의 (1,2) 에서도 좋은수에 카운트되고, 뒤의(1,2)에서도 카운트 된다
-> 해결 : vis[LB]를 만들고, 이미 좋은수로 체크된경우 pass 하도록 했다.
3. 문제 : 이분탐색 주의점 : idx 가 i, j와 같은경우 예외처리에 심혈을 기울이도록 하자.
2. 내코드
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll ret;
int n,vis[2004];
vector<ll> v;
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n;
for(int i=0;i<n;++i){
ll tmp;
cin >> tmp;
v.push_back(tmp);
}
sort(v.begin(), v.end());
//for (auto i : v) cout << i << " ";
//cout << "\n";
for (int i = 0; i < n-1; ++i) {
for (int j = i + 1; j < n; ++j) {
ll cur = v[i]+v[j];
//cout << i << " " << j << "\n";
int LB = lower_bound(v.begin() , v.end(), cur) - v.begin();
int UB = upper_bound(v.begin(), v.end(), cur) - v.begin();
//해당수가 존재하는경우
if (UB - LB) {
//cout << i << " " << j <<" " << v[LB] << "\n";
if (vis[LB]) continue; //해당수는 이미 좋은수인경우 패스
if (i == LB || j == LB) continue;
ret += (UB - LB);
vis[LB] = 1;
}
//ret += (UB - LB);
//cout << i << " " << j << "\n";
//int idx = lower_bound(v.begin() + i + 1, v.end(), cur) - v.begin();
//for (int k = -1; k <= 1; ++k) {
// if (idx + k < 0 || idx + k >= n) continue; //범위쳌
// if (idx + k == i) continue; //자기자신제외
// if (abs(ret) > abs(cur + v[idx + k])) { //정답갱신
// ret++;
// }
//}
}
}
cout << ret;
return 0;
}
3. 문제 : 내코드는 뭔가 중복이 많고 예외처리가 많아 복잡하다.
4. 바킹독 의사코드
1. 함수 solve(i) // a[i]가 좋은수인가?
2. x + a[j] = a[i]를 만족하는 x가 존재하면 -> a[i]는 좋은수이다.
ex) 1 2 3 3 3 4
i j (이때 x+2=1 인 x(-1)가 존재하면 1은 좋은수이다.)
3. x의 idx를 LB로 찾음
4. 범위쳌(x가없는경우 out of 에러) && a[idx]==x(찾은경우) ret++후 return 하면된다.
5. while문과 idx++을 두는 이유는 자기자신을 가르키지 않기 위함인듯하다
ex ) 0 0 0 0 0 0 1
i j
(idx==i) ----->
5. 바킹독 전체코드
// Authored by : scsc3204
// Co-authored by : -
// http://boj.kr/cf7ce676aad54a2786941423afd99612
#include <bits/stdc++.h>
using namespace std;
int cnt, n;
vector<int> a;
void solve(int i) {
for(int j = 0; j < n; j++) {
if(j == i) continue;
int x = a[i] - a[j];
int idx = lower_bound(a.begin(), a.end(), x) - a.begin();
while(idx < n && a[idx] == x) {
if(idx != i && idx != j) { cnt++; return; }
idx++; //자기자신이 아닌놈 가리키기 위해 ++
}
}
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n;
for(int i = 0; i < n; i++) {
int x; cin >> x;
a.push_back(x);
}
sort(a.begin(), a.end());
for(int i = 0; i < n; i++) solve(i);
cout << cnt;
}
* 25.3.24. 2회독
* 시도0(완탐, 오답)
- map에 두면될듯?
- 반레 : 중복계산 방지 어려움
- 3중 for문에서 for(k)를 이분탐색으로 줄인다면?

* 시도1(오답)
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int n,ret;
int arr[2004], vis[2004];
map<int,int> m;
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
cin>>n;
for(int i=0;i<n;++i) {
cin>>arr[i];
}
sort(arr,arr+n);
for(int i=0;i<n;++i) {
for(int j=i+1;j<n;++j) {
int sum = arr[i] + arr[j];
int idx = lower_bound(arr , arr+n, sum)-arr;
if(idx < n) {
// cout<<sum<<" ";
while(arr[idx] == sum) { // (idx++은 완탐임) 이걸 줄여야함! upper bound 로!
if(vis[idx]) continue;
vis[idx]=1;
ret++;
idx++;
}
}
}
}
cout<<ret;
return 0;
}
* 시도2 (정답)
- 이때 if 문을 ub-lb로 해야한다.
- ub와 lb가 달라야 찾은것!
- lb > n 만으로 불충분
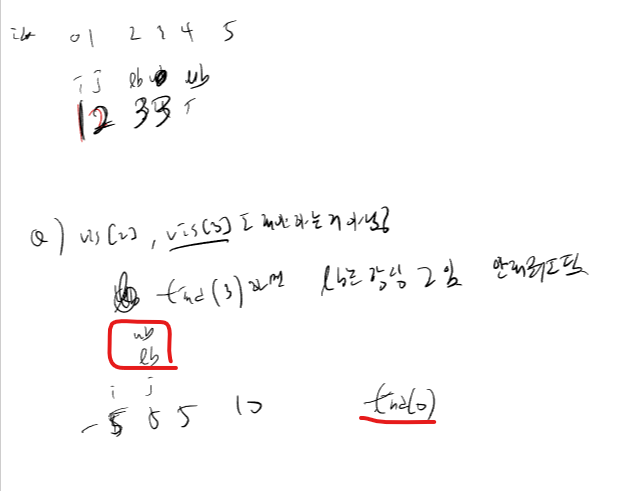
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int n,ret;
int arr[2004], vis[2004];
map<int,int> m;
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
cin>>n;
for(int i=0;i<n;++i) {
cin>>arr[i];
}
sort(arr,arr+n);
for(int i=0;i<n;++i) {
for(int j=i+1;j<n;++j) {
int sum = arr[i] + arr[j];
int lb = lower_bound(arr , arr+n, sum)-arr;
int ub= upper_bound(arr , arr+n, sum)-arr;
if(ub-lb > 0) {
// cout<<sum<<" ";
if(vis[lb]) continue; //증복체크 방지
if(i==lb || j==lb)continue; //자기자신은 제외
ret += (ub-lb);
vis[lb]=1;
}
}
}
cout<<ret;
return 0;
}
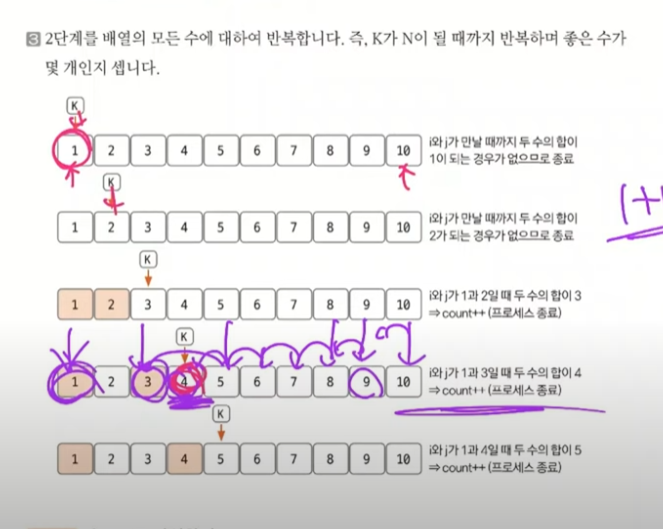
* 시도3 (투포)

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int n,ret;
int arr[2004], vis[2004];
map<int,int> m;
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
cin>>n;
for(int i=0;i<n;++i) {
cin>>arr[i];
}
sort(arr,arr+n);
for(int k=0;k<n;++k) {
int s=0;
int e=n-1;
while(s<e) {
int sum = arr[s]+arr[e];
if(sum == arr[k]) {
//자기자신은 안됨!
if(s!=k && e!=k) {
ret++;
break;
}
if(s==k) { //같은데, 자기자신인경우들은 정답이아님. 포인터갱신
s++;
}
else if(e==k) {
e--;
}
}
else if( sum > arr[k]) {
e--;
}
else {
s++;
}
}
}
cout<<ret;
return 0;
}
'Algorithm > 이분탐색' 카테고리의 다른 글
| 프로그래머스 연속된부분수열의합 c++ // 정렬된 입력은 이분탐색, 누적합 (0) | 2024.04.16 |
|---|---|
| 백준 7453 합이0인네정수 c++ // 이분탐색 갯수세기는 ub-lb (0) | 2024.03.30 |
| 백준 14921 용액합성하기 c++ // 이분탐색 정석패턴 (0) | 2024.03.26 |
| 백준 2473 세용액 c++ // 이진탐색 패턴정석 외우기 (0) | 2024.03.25 |
| 백준 3151 합이0 c++ // 이분탐색, nC3최적화하는법 (0) | 2024.03.25 |


