Mini
[맞음] 백준 2293 동전1 c++ // dp, 경우의수는 덧셈이다! 본문
https://www.acmicpc.net/problem/2293
2293번: 동전 1
첫째 줄에 n, k가 주어진다. (1 ≤ n ≤ 100, 1 ≤ k ≤ 10,000) 다음 n개의 줄에는 각각의 동전의 가치가 주어진다. 동전의 가치는 100,000보다 작거나 같은 자연수이다.
www.acmicpc.net
1. 의사코드
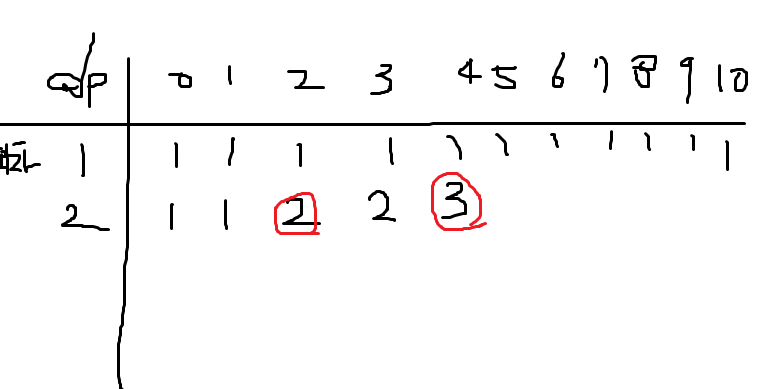
여기에서 2회차 dp[4]를 보면
1111
112
22 의 경우의 수가 있는데,
1111은 1회차의 dp[4]의 경우의수이고 (1)
11, 2 는 2회차 dp[2]의 경우의수이다. (2)
답은 1+2 = 3
따라서 dp[4]=dp[4](이전회차 경우의수) + dp[4-2(coin)] (현재회차까지 동전으 직전코인 경우의수) 이라는 식이 도출된다.
2. 경우의수는 덧셈이다.

dp[4]를 구하는 경우의수 : 이전dp[4] (1) 에서 오는 경우의수 + dp[2]에서 오는경우의수 == 3이다.
두 경우를 더하면 된다.
아래에 새 노드가 추가되면 그 경우의수를 더하면 된다.
3. 전체코드
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int d[10000 + 1]; //d[i] : i원을 만드는 경우의 수
int n, k, coin[100 + 1];
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n >> k;
d[0] = 1;
for (int i = 0; i < n; ++i) {
cin >> coin[i];
}
//d: 0 1 2 3 4 5 6 7 8 9 10 을
//여러번(동전갯수n만큼) 왕복하면서 갱신!
//
//d[4]=d[4](이전경우의수) + d[2==4-2(coin)]
for (int i = 0; i < n; ++i) {
for (int j = 1; j <= k; ++j) {
if (j - coin[i] >= 0)
d[j] = d[j] + d[j - coin[i]];
else
d[j] = d[j];
}
}
cout << d[k];
return 0;
}
4.리팩토링
ex) 2원이면 k=0,1일때에는 당연히 경우의수가 0이다.
-> 탐색을 coin부터(2원부터) 탐색한다.
이러면 out of index 체크도 안해도된다.
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int d[10000 + 1]; //d[i] : i원을 만드는 경우의 수
int n, k, coin;
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n >> k;
d[0] = 1;
//d: 0 1 2 3 4 5 6 7 8 9 10 을
//여러번(동전갯수n만큼) 왕복하면서 갱신!
//
//d[4]=d[4](이전경우의수) + d[2==4-2(coin)]
for (int i = 0; i < n; ++i) {
cin >> coin;
for (int j = coin; j <= k; ++j) {
d[j] += d[j - coin];
}
}
cout << d[k];
return 0;
}
* 2회독 (23.3.17.)

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int n,k;
ll dp[10000+4];
int main(){
ios_base::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
cin>>n>>k;
fill(dp,dp+10000+4,0);
dp[0]=1; // 패딩을 1로해야 식이 맞음
for(int i=0;i<n;++i) {
int tmp;
cin>>tmp; //2원
for(int j=tmp;j<=k;++j) { //tmp부터 시작하면 범위검사 필요없음
if(j-tmp>=0) {
dp[j]=dp[j]+dp[j-tmp];
}
}
}
cout<<dp[k];
}'Algorithm > dp' 카테고리의 다른 글
| 백준 2225 합분해 c++ // dp 규칙찾는 방법 (0) | 2023.11.29 |
|---|---|
| [틀림] 백준 2294 동전2 c++ // dp 동전논리 정리, 규칙성발견 dp테이블 형식, 나누기보다는 덧셈 (0) | 2023.11.29 |
| 백준 9251 LCS c++ // DP 푸는방법 : 1. 부분해->전체해 2. DP테이블 그리기 (0) | 2023.11.26 |
| [맞음] 백준 12865 평범한 배낭 c++ // dp는 경우의수로 해결, ox dp (0) | 2023.11.26 |
| 프로그래머스 코딩테스트공부 c++ // dp, 예외처리방법 (0) | 2023.11.19 |





